Verdwijnend oppervlak

         

         

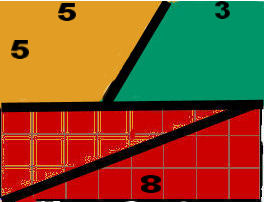
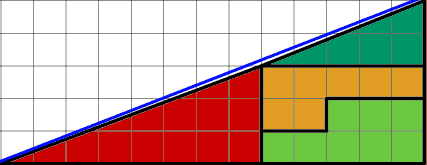
William Hooper kwam in zijn boek met de titel Rational Recreations (1774) als eerste met een wiskundig raadsel waar een oppervlak dat er niet zou moeten zijn, er toch is. Dat valt als volgt te berekenen: in principe is het oppervlak van de linker figuur gelijk aan 8² = 64 hokjes. Maar volgens een andere berekening van een vlak samengesteld met hetzelfde driehoekje en 2 trapezia, zou je ook kunnen rekenen: 5 x 13 = 65 hokjes. Waar komt nu dat ene hokje extra vandaan?

         

In de tekening rechts is dat oppervlak tussen de blauwe en de zwarte lijn geklemd. Het merkwaardige is dat er rekenkundig een ruimte ontstaat, die er eigenlijk niet had mogen zijn. Dit komt, volgens wiskundigen, omdat de zijden voor  lengte en breedte overeenkomen met de getallen van Fibonnacci: 1 1 2 3 5 8 13 21etc. Deze hebben de eigenschap dat het product van twee van deze getallen steeds met 1 verschillen. Hierdoor lijken de verhoudingen tussen de zijden 5/13 = 0,384 en 3/8 = 0,375 bijna gelijk aan elkaar, maar ze zijn het in feite niet. De verschillen zijn zo klein dat je ze niet ziet in de tekening. Door de zijden over de vierhoeken anders te verdelen, komt er dan een ander oppervlak uit.

         

Het is dit principe waardoor je het idee krijgt dat als de zijden zoals in de animatie voortdurend met elkaar verwisselen er ruimte moet ontstaan. Door deze ruimtes kunnen de sappen met elkaar mengen. Maar ook kan de man of vrouw die een voorspelling wil doen een kijkje nemen in de “hemel” Dit is dan nog weer een aanvulling op de gedachte dat een platvlak zich vervormen moet om zich om een bol heen te kunnen wikkelen.

         

Literatuur:

         

1. Brian Greene: De Ontrafeling van de kosmos (The fabric of the Cosmos), een zoektocht naar de theorie van alles,  Spectrum, 2005.

         

2. Brian Greene: De kosmische symfonie, Arbeiderspers, Amsterdam, 2001 (The elegant universe, Vintage, 2000, New York).

         

3. Martin Kindt en Ed de Moor, Wiskunde in de notendop, Bert Bakker, 2008.

         

4. De Werelden van M.C. Escher, Meulenhoff Amsterdam, 1971.

         

7. David Wells, Book of Curious & interesting puzzles, Dover publications, inc. , Mineoloa, New York, 1992, pag. 41-42 en de oplossingen pag. .