Het geheugen
De afgelopen tijd wordt er veel geschreven over het geheugen. Ik heb daarover de volgende twee boeken gelezen: “Ben ik dat” van Mark Mieris, en van Dick Swaab, “Wij zijn ons brein”. Ik ben geen neurowetenschapper of bioloog en zal het dan ook niet wagen om het met een van beide heren oneens te zijn. Wat mij opviel, is dat ze beiden het eens zijn over het belang van een bepaald deel van de hersenen, de hippocampus, voor het geheugen, voor het verleden, maar ook voor de toekomst, en wel in samenhang met ons gevoel voor ruimtelijke oriëntatie. Mieris zegt het in de volgende bewoordingen: "..herinneringen en toekomstbeelden (komen tot stand) op dezelfde manier". En Swaab "…… de hippocampus (is) niet alleen cruciaal voor ons geheugen, we hebben hem ook nodig voor onze ruimtelijke orëntatie en om onszelf een coherente voorstelling van de toekomst te kunnen maken.." Bij herlezing, dacht ik: dat is gewoon rekenen………wiskunde! De tijdsrekening..in een ruimtelijk verband, zoals het kwadraat van twee getallen een vierkant oplevert, en de verheffing tot de derde macht van dezelfde getallen in een doos (koffer) van die afmetingen resulteert, en tenslotte de verheffing tot de vierde macht merkwaardig genoeg een driedimensionaal object oplevert etc. Het levert o.a. ook de zogenaamde platonische veelvlakken op met patronen zoals je die vaak terugziet in Marokkaanse, Turkse of Iraanse etc kunst. Dat moet dus gewoon goed zijn voor je geheugen om veel van dit soort patronen om je heen te zien! 
Dit is dus een verband tussen geheugen, toekomst, getal en verhaal! Maar hoe zit dat verband nu precies in elkaar. Een voorbeeld treffen we aan in het boekje van Dominic O'Brien, Leer te Onthouden, in het hoofdstuk Mnemoniek (geheugensteuntje), pag. 95. Hij vraagt de lezer om een ezelsbruggetje (!) voor het getal "pi" (3,141592653589) te bedenken en suggereert dan zelf het volgende zinnetje:"Wie (3) u (1) kent (4), o getal, wonderlijk en gepast, heeft een sterk geheugen ijzervast (9)". Zou er met onze grappige verhaaltjes hetzelfde het geval kunnen zijn? Al vanaf het eerste verhaal dat in Deel 2 wordt geciteerd, speelt het spelen met cijfers een rol: 3 verdiepingen, die op ongelijke hoogte van elkaar staan. Ook bij de auberginekoopman gaat het erom te kunnen tellen, en als je niet op je tellen past, dan worden je knollen voor citroenen verkocht. In een Egyptisch verhaaltje speelt Pascal een rol: 1 en 1 is 2; 1,2 en 1 is 4; 1,3,3 en 1 is 8...etc. Als je het verhaal erop na wilt lezen, klik dan hier op de titel van het verhaal: Het konijn is aan ons voorbij gegaan (Is het konijn in een soort Pascaliaanse piramide begraven?). Toch is duidelijk dat hier op een andere manier de geheugensteun tot stand komt dan door het simpel tellen van de letters van een tekst.
Toch is duidelijk dat hier op een andere manier de geheugensteun tot stand komt dan door het simpel tellen van de letters van een tekst.
Als we bijvoorbeeld de tekst van Apuleius erbij nemen, ontdekken we dat hierin ook weer sprake is van getallen: niet 6 denariën is de koopprijs voor het vat (inhoudsmaten van vaten, potten, dozen, koffers, zakken en manden etc spelen een grote rol in deze verhaaltjes), maar 7 denariën (met collateral damage). Als je het verhaal visualiseert, om er achter komen wat er nou zo moeilijk te onthouden moet zijn geweest, dan doemt het beeld van de hand-oliepers,  de tahuna, in mijn gedachten op. Dit zijn twee ronde kleine molensteentjes op elkaar geplaatst, met midden in de bovenste een gat waarin de olijven kunnen worden gedaan, en eveneens in de bovenste steen, meer naar de rand toe een houten pin om deze op de onderste molensteen rond te kunnen draaien. Een sleuf in de onderste steen zorgt ervoor dat de geperste olijven, de olie, in een kom kan worden opgevangen. Maar wat is er nu zo moeilijk aan deze handmolen te onthouden, mocht je de techniek om hem te maken voor de generatie na jou willen behouden? Ik denk dat het antwoord zit in de ribbels die zitten aan de onderkant van de bovenste steen en aan de bovenkant van de onderste steen, waardoor de molenstenen beter op elkaar blijven draaien. Zou daarin de verhouding 6/7 een rol in kunnen spelen? Of het heeft iets met de helling, de hoek waarin de bovenste steen past in de onderste te maken? Als je de oudste wiskundige puzzles in het boek van David Wells erop naslaat dan komt het bepalen van de invalshoek, het berekenen van de hoek van een bouwwerk etc vaak voor in dit soort hersengymnastiek. Dit is natuurlijk de eerste handeling om van 1 grote steen 2 aparte molenstenen te maken! Eigenlijk is het zelfs een klein beeldhouwwerkje, en om het goed te laten werken moeten de stenen perfect op elkaar passen, anders kun je er niet mee malen.
de tahuna, in mijn gedachten op. Dit zijn twee ronde kleine molensteentjes op elkaar geplaatst, met midden in de bovenste een gat waarin de olijven kunnen worden gedaan, en eveneens in de bovenste steen, meer naar de rand toe een houten pin om deze op de onderste molensteen rond te kunnen draaien. Een sleuf in de onderste steen zorgt ervoor dat de geperste olijven, de olie, in een kom kan worden opgevangen. Maar wat is er nu zo moeilijk aan deze handmolen te onthouden, mocht je de techniek om hem te maken voor de generatie na jou willen behouden? Ik denk dat het antwoord zit in de ribbels die zitten aan de onderkant van de bovenste steen en aan de bovenkant van de onderste steen, waardoor de molenstenen beter op elkaar blijven draaien. Zou daarin de verhouding 6/7 een rol in kunnen spelen? Of het heeft iets met de helling, de hoek waarin de bovenste steen past in de onderste te maken? Als je de oudste wiskundige puzzles in het boek van David Wells erop naslaat dan komt het bepalen van de invalshoek, het berekenen van de hoek van een bouwwerk etc vaak voor in dit soort hersengymnastiek. Dit is natuurlijk de eerste handeling om van 1 grote steen 2 aparte molenstenen te maken! Eigenlijk is het zelfs een klein beeldhouwwerkje, en om het goed te laten werken moeten de stenen perfect op elkaar passen, anders kun je er niet mee malen.
De hier gepresenteerde geheugentechniek is zoals al gezegd door Cicero in de belangstelling gekomen. Een krantenartikel met als lead ”Oude Sanskrietverzen zingen van wiskunde“ in de NRC van zaterdag 16 april, suggereert echter dat de oorsprong ervan nog weleens veel ouder kan zijn. Kim Plofker (wetenschapshistoricus) beweert dat ook in oude Sanskriet teksten wiskundige formules verstopt zitten, net zoals in onze verhaaltjes. Zij plaatst deze teksten binnen de astrologie en heilige altaren. Dus alweer wordt voor het geheugen in de ruimte een plaats ingericht. Hoewel nog steeds veel mensen denken dat met de uitvinding van de nul ook de uitvinding van het tientallig stelsel samenvalt, is dit niet zeker. Zeker is in ieder geval dat de oudste "nul" in Gwalior in India is gevonden, gedateerd 876 vóór Christus! Het tientallig stelsel is bij ons veel later bekend geraakt via de Arabieren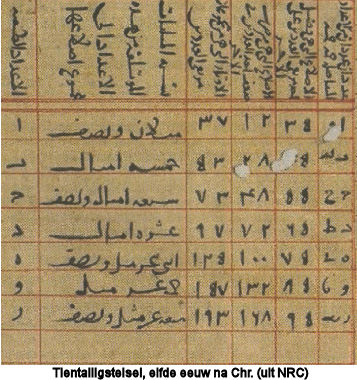
In onze teksten is er telkens weer sprake van twee getallen die 1 van elkaar verschillen: het verhaal met de verdiepingen, het verhaal met de aubergines en ten slotte het Apuleius verhaal. Dat verschil zou weleens te verklaren kunnen zijn uit het verschil tussen de wijze waarop de Romeinen rekenden en het tientallig stelsel. De Romeinen kenden in feite maar 9 symbolen om hun getallen te noteren (rekenen deden ze met een abacus en was heel visueel).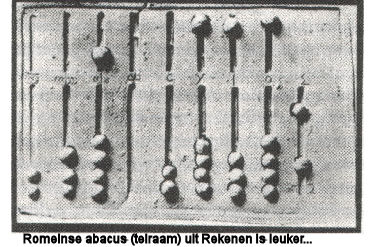 In het tientallig stelsel is er door de toevoeging van de "nul" een tiende symbool bijgekomen. Dat houdt in dat er bij de vertaling van de berekening van het ene stelsel in het andere er steeds een verschil van 1 is. De redenatie is niet zomaar een gelukkige greep, omdat juist het hierboven aangehaalde verhaal over het konijn dat de geest heeft gegeven, met daarin de piramide van Pascal, dit verschil van 1 niet kent. Waarom niet, omdat het hier om visueel rekenen gaat dat je zo op een telraam (abacus) kunt uitzetten!
In het tientallig stelsel is er door de toevoeging van de "nul" een tiende symbool bijgekomen. Dat houdt in dat er bij de vertaling van de berekening van het ene stelsel in het andere er steeds een verschil van 1 is. De redenatie is niet zomaar een gelukkige greep, omdat juist het hierboven aangehaalde verhaal over het konijn dat de geest heeft gegeven, met daarin de piramide van Pascal, dit verschil van 1 niet kent. Waarom niet, omdat het hier om visueel rekenen gaat dat je zo op een telraam (abacus) kunt uitzetten!
Het verschil van 1 is een aanwijzing dat de verhaaltjes oud zijn, en dat er verschillende wiskundige formules in verstopt zouden kunnen zitten. Welke dat precies zijn is niet meer te achterhalen, tenminste meestal niet. Dat de verhalen dienden om zich bepaalde technieken en maten te herinneren, staat voor mij wel vast.
Literatuurlijst:
- Wij zijn ons brein van Baarmoeder tot Alzheimer, Dick Swaab, 2010, Bariet, Ruinen.
- Ben ik dat, Wat hersenonderzoek vertelt over onszelf, Mark Mieras, 2007, Nieuw Amsterdam uitgevers.
- Leer te Onthouden, Dominic O'Brien, 2005, Librero.
- Book of Curious & interesting puzzles, David Wells, 1992, Dover Publications, Minola/New York.
- Wiskunde in een notendop, Martin Kindt en Ed de Moor, 2008, uitgerij Bert Bakker, Amsterdam.
- Rekenen is leuker dan/als je denkt, Marjolein Kool en Ed de Moor, uitgeverij Bert Bakker, 2010.